
Evaluation of Active Balancing Circuits for Supercapacitors
- Posted by doEEEt Media Group
- On February 9, 2023
- 0
Abstract
Supercapacitors are strongly emerged as a promising technology to complement the batteries. Due to their low rated voltages it is usual to build supercapacitor banks, with series connection, in order to obtain higher voltage levels. Because of manufacturing dispersion parameters, during operation in multiple charge-discharge cycles it is very probable to result an uneven state of charge (SOC). During charging at constant current the capacitor that reaches first the rated voltage level could be damaged in a further charging process.
In order to prevent this, additional circuitry, named briefly, balancing circuit is provided. The balancing circuit with resistors and diodes are a simple solution, but with high power losses and modest performances. An improved solution is to use transistors to bypass the charging current, when an overvoltage is detected at each capacitor terminals. An even better solution is to use smart control using microcontroller or dedicated circuits for monitoring the series connection of supercapacitors.
We present in this paper our experience based on a dedicated integrated circuit. The circuit was developed by TI based on circuits already in use for Li ion batteries. The integrated circuit bq33100 [1] provides more than balancing of supercapacitor banks, being a single-chip solution that provides many features for charge control, monitoring, and protection of maximum 5 series capacitors. The circuit bq33100 can be programmed to determine periodically or at command the capacitance and equivalent series resistance (ESR) of the supercapacitor series group during normal operation. We will present the results that proved the effectiveness of balancing for a bank that uses 5 capacitors of 22F, starting from different SOC at each capacitor and for different charging currents. The test board built around the circuit is performant, energy efficient and can be further improved to ensure the balancing control for larger capacitance, by increasing the charging and bypass current.
Introduction to Capacitor Charge Balancing
Supercapacitors or EDLCs are now seen as a promising energy storage alternative to batteries, but not only. A particular drawback of supercapacitors is their low-rated voltage. The usage in automotive applications at a rated voltage of about 14V requires a series connection, typical of six (or five) individual EDLCs’, usually called cells. In this way, the valuable capacitance is reduced to C/6 (or C/5) see Fig. 1.
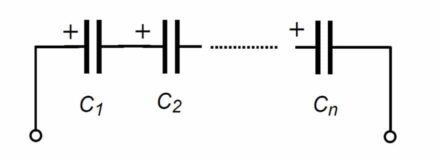
Fig 1. Series connection of supercapacitors (cells) to form a supercapacitor module (SM) or a battery
To increase the capacitance in a series connection, constructing a supercapacitor module (SM) also using parallel links is necessary. This parallel connection is also helpful for reducing the module’s equivalent series resistance (ESR) [2]. In an SM, the SOC of each cell will probably be unequal in a simple operation under load and multiple charge-discharge cycles.
A cell that presents a higher capacitance will show a reduced SOC (or voltage). The uneven distribution will be more evident during the charging process. The charging process of series-connected capacitors is affected by the nonequal capacitance values. The EDLC as an electronic component is subject to inherent variation of parameters from device to device, for instance, the capacitance, the leakage current, or the ESR (Equivalent Series Resistance).
These differences in capacitance are caused by manufacturing variances or are caused by aging. The supercapacitor capacitance could vary up to ±20% of the rated value. This capacitance variance can create a variation in the voltage of the supercapacitor during the charge-discharge process (dynamic). Voltages of individual capacitors during a charging process with the current I0 can be written as:
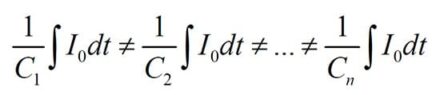
With C1 to Cn, the device’s capacitance is 1 to n, respectively.
During the pauses in the charge-discharge process, the different values of the leakage current of capacitors can create a dispersion of the individual capacitor voltages (static), defined as:
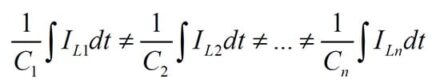
Where IL1 to ILn is the leakage current of capacitors 1 to n, respectively.
And last but not least, the variation in the values of the capacitor’s ESRs also creates some dispersion (dynamic) in the individual voltages when the supercapacitor series connection is submitted to the charge-discharge process. The resulting voltages are:
R1 to Rn is the ESR of the capacitor 1 to n, respectively, and I0 is the charging current.
From (1), during charging with constant current, the capacitors with greater capacitance will be charged to lower voltages, and the capacitors with smaller capacitance will be charged to higher voltages. So, the voltage distribution initially depends on capacitance values, and when the charging is ended, it depends on the leakage current.
If the charging circuit has voltage compliance set to the sum of the rated voltages of capacitors, there is the risk that some capacitors will be charged above the voltage limit. It is necessary to use some methods to prevent this fact. The simplest passive way for achieving a voltage balance is the circuit shown in Fig. 2. The balancing course uses for each capacitor C1 to Cn a resistor R1 to Rn, connected in parallel to it.
The values of resistances are chosen according to the supercapacitor leakage current. This parallel connection of resistors is widely used for series-connected electrolytic capacitors. This resistive balancing circuit can balance the voltages in the stand-by regime and provides no dynamic balancing. Another drawback is the energy loss during the charging-discharging process, which limits the usage of the circuit in low-power applications or low charge/ discharge rates.
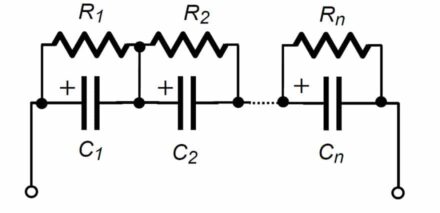
Fig. 2. Passive balancing circuit with resistors
Another method for balancing the SM voltages is the circuit presented in Fig. 3. The course consists of Zener diodes DZ1 to DZn parallel connected to supercapacitors instead of resistors. The diode limits the maximum charging voltage of a capacitor due to clamping voltage. This circuit has the advantage over the resistive one in that there are no power losses before the capacitor has reached the rated voltage and is in the stand-by regime.
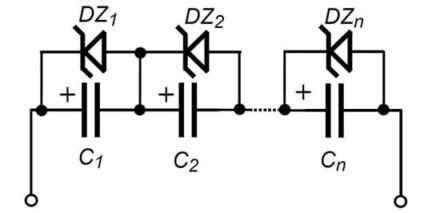
Fig. 3. Passive balancing circuit with Zener diodes (Clamping Diodes)
The main disadvantage of this balancing circuit is the lack of dynamic voltage balancing capability. It would be possible to achieve dynamic voltage limiting, but it would require high-power clamping diodes. The difficulties in implementing the circuit come from low-voltage Zener diodes (2.4-2.6V).
High current and high power Zener diodes are not available in this voltage range. Supplemental, the diodes breakdown voltage Vz is affected by large parameter dispersion and exhibits significant temperature variations. A better circuit should perform automatic voltage balancing and prevent the over-voltage occurrence of individual supercapacitors in series connection while maintaining the charging current for the SM.
The solution for this balancing circuit presented in Fig. 4 is based on switched resistors. The course consists of resistors and switches SW1 to SWn. The
resistors R1 to Rn are connected in parallel with the capacitor C1 to Cn using the switches SW1 to SWn.
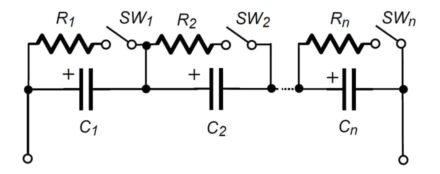
Fig. 4. Automatic balancing circuit with switched resistors
The capacitors’ voltages are monitored, and if the voltage increases above a pre-established threshold (2.5V, for instance), a command is given to the switch. This way, the charging current is diverted through the resistor. After the capacitor voltage has been naturally reduced (due to self-discharge) to a value below the reference voltage, the switch will be turned off.
Resistors have some power losses when the switch is on, but this circuit is a good balancing solution. A solution to implement this circuit is to use transistors as bypass switches and voltage references for comparing the capacitor voltages with the chosen threshold. The schematic of a balancing circuit built using this principle is shown in Fig. 5 a), and a picture of the practical realization is in Fig. 5 b). [3]

Fig. 5. a) Schematic drawing of the balancing circuit. b) The supercapacitor module (SM) with six 200F/2.7V capacitors
and balancing circuits attached
The circuit was designed for a voltage of about 2.62 V and a bypass current of up to 1A. The heat dissipation determines the limitation in the current domain in R1 and Q2. The operation principle is based on diverting the charging current through a resistor (R1) and a transistor (Q2), as presented in the previous section.
When the voltage at the capacitor terminals reaches the preset limit, the transistor Q1 begins to conduct the current through it, leading to the opening of transistor Q2. Transistor Q1 is a tiny SMD transistor BC807-40, and Q2 is a high current, high power FZT849. The resistor R7 provides positive feedback that accelerates the switching of transistor Q2.
The voltage reference is provided by the precision band-gap reference circuit LM4004 and was internally set to 2.048V. The LED is intended as an indicator and will be on when Q2 is turned on; this means when the balancing circuit is active. A better solution is represented by the newly developed intelligent courses for supercapacitor charging and control. A solution based on the principle shown in Fig. 4 is presented in the next section.
II. Intelligent Balancing Circuit Operation Mode
In our implementation of an intelligent balancing circuit we have used the integrated circuit bq33100 [1] which provides not only balancing of supercapacitor modules. It is in the same time a single-chip solution that provides many features for charge control, monitoring, and protection. It can individually monitor either 2, 3, 4, or 5 series of supercapacitors with individual balancing or up to 9 series capacitors with less control, only the stack voltage being measured. The bloc diagram of the system built around bq33100 is presented in Fig. 6.
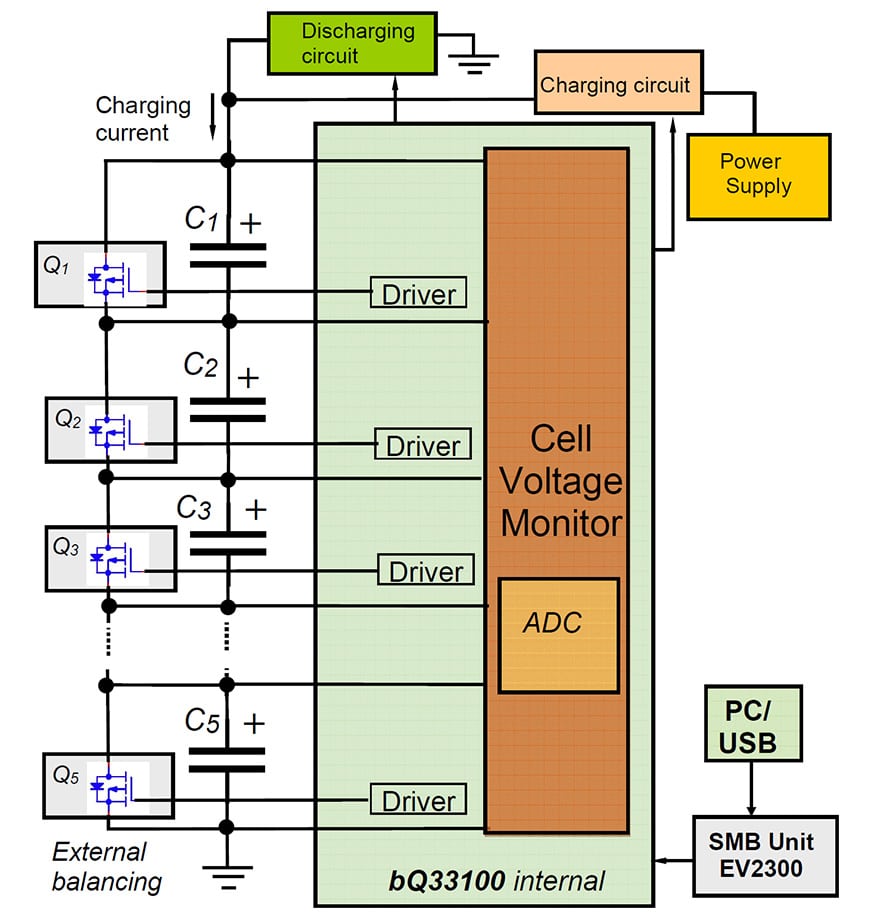
Fig. 6: Bloc diagram of the active balancing and monitoring circuit based on bq33100 chip
We have used an evaluation board from Texas Instruments (TI), built around the circuit bq33100. The board is set to charge a series connection of five supercapacitors. The system includes a communication SM Bus adapter for connecting with a PC via a USB port and a power supply. A specific but customizable free software package from TI was also used [4].
The detailed schematic of the system is presented in Fig. 7. This is based on design recommendations and application notes from [1]. The power supply voltage of the board must be high enough to ensure the charging voltage of the supercapacitors bank (>n× 2.5V), n being the number of series connected supercapacitors in the bank, or to ensure the minimal power supply of the IC.
The right side of the circuit is responsible for charging. The stabilizer Q1 and the circuit D2, type TL431, a precision reference voltage set the voltage for charging. The pMOS transistor Q6 controls the charging process. There exists the possibility to use four charging voltages by controlling the on-off state of transistors Q2 and Q3; their gates are connected to the controlling circuit. The four possible voltage levels are 10.5, 11.1, 11.8, and 12.4 Volts.
Usually, during charging, we have always used the maximum level; the other groups are being used by the bq33100 circuits for other purposes, for instance, the learning process that was previously mentioned. The maximum Charging current is set by the values of resistors R2 and R3 connected accordingly to reference circuit D1. In the present implementation Imax=Vref/Req with Vref=2.5V, a typical value for D1, and Req=10Ω/2=5Ω. It results in a maximum Charging current of 500mA.
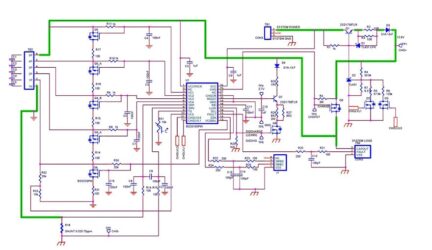
Fig. 7. Complete schematic diagram of the supercapacitor evaluation board using the circuit bq33100
In the supercapacitor module, the capacitors are connected in series and are attached externally at connector TB2. The expected points between two adjacent capacitors are connected to the pins of IC bq3310 using the resistors R8-R11, with the required value of 1kΩ. The pins VC1-VC5 of the IC are used for voltage monitoring and balancing control. The exception here represents the terminals of the capacitor C5, for which two pins are provided: one for voltage monitoring (pin 10- VC5) and the other pin (pin 13-VC5BAL) used for command of the balancing process.
The IC achieves high measurement accuracy using a 16-bit delta-sigma ADC with 16-channel multiplexing. The ADC is used for measuring all the individual capacitor or whole bank voltages, the charge/discharge current, and temperature measurement using the thermistor TH1. the current through the bank is measured using R18, a shunt resistor having 20mΩ.
The balance is achieved by driving the five pMOS transistors Q4 A and B, Q5 A, B, and Q9. The load resistances are represented by R14-R17 and R31, having a value of 100Ω. This leads to a balancing current of 25mA, about the 20th part of the maximum Charging current. Higher balancing currents are possible by lowering the resistance values. This leads to higher balancing speed at the expense of higher dissipation and more powerful MOS transistors.
Primarily built for measurements of capacitance and ESR, the board disposes of a discharge circuit built around Q7, Q8, R28, R27, R26, and D4. The bipolar junction transistor Q7 ensures the constant current, R27 and R28 are the sink load, and Q8 is the switch for driving the discharging. Diode D4 is used for protection reasons. Without D4, when the voltage of the supercapacitor module is low, the pin REG27 of the IC is always at 2.7V, and the base-collector junction of Q7 can be directly biased.
The integrated circuit bq33100 can be programmed to determine at certain time intervals or specific commands the supercapacitor module’s capacitance and equivalent series resistance (ESR) during normal operation. This process is called “Learning.” The main steps of this procedure, fully controlled by the IC, are presented in Fig. 8. The integrated circuit bq33100 performs the following sequence to determine Capacitance and ESR:
- Charge to V Learn Max, a value typically smaller than Vmax of supercapacitors, 2.4 V for a single cell, so 12 V for a five supercapacitor series module
- Discharge using constant current load (up to 500mA) to a specific voltage and record voltage and time
- Charge up to V Learn Max,
- Discharge using constant current load and internally record current and time
- Calculate Capacitance and ESR based on recorded voltage and current
- Determine new Charging Voltage for regular operation (5×2.4V )
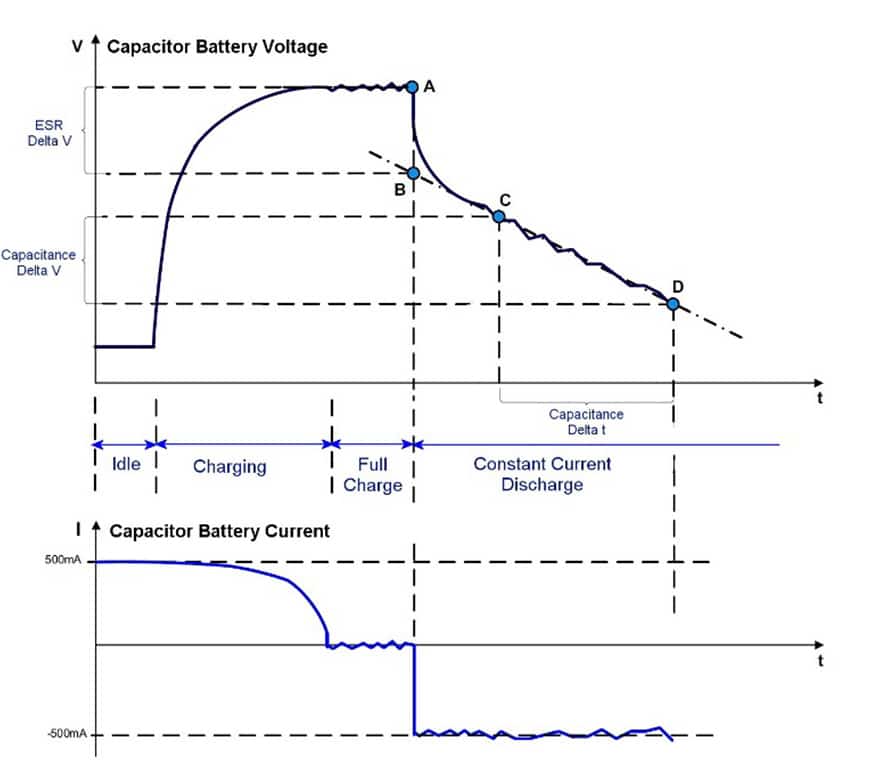
Fig. 8. Cycles used by the circuit for capacitance and ESR measurement (learning)
With the marked points in Fig. 8, we can use (4) and (5) to calculate the capacitance and ESR, respectively.

To ensure serial communication, a commercially available SMBus module EV2300 [5] from TI was connected at connector J1.
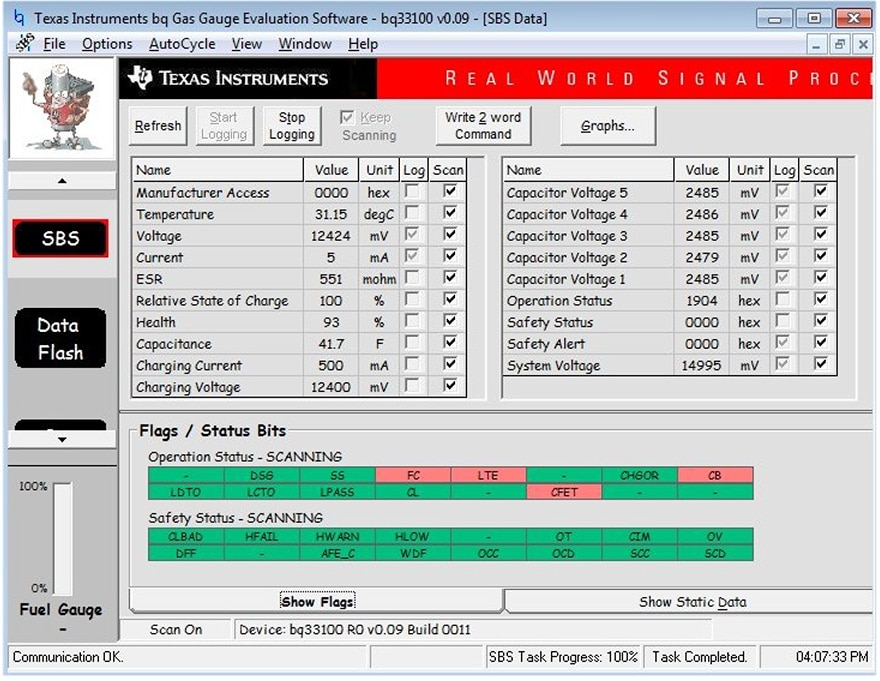
Fig. 9. Screen of the software bqEVSW showing the capacitor voltages, the charging conditions, and the flag registers
To communicate with the evaluation board, we have used a free evaluation software from TI, called bqEVSW [4],[6], which can change the registers of bq33100 and set different parameters for operation. Most of the default parameters do not need to be changed. We have changed the parameters for charging current, over-voltage, and over-current protection.
The software of the IC uses advanced algorithms and the actual measured data to determine the SOC and available capacitance of the supercapacitor bank. A part of the working screen of bqEVSW is shown in Fig. 9. The voltages at each capacitor, the almost finished balancing process, and the flag registers FC- Full Charge, and CB can be seen- Capacitor Balancing being set (red color).
III. Results
We have tried the effectiveness of balancing for two capacitor banks, one uses 5 capacitors of 22F and the second bank having 5 series of 200F supercapacitors. The effective capacitance is 4.5F, respectively 40F. We have used a maximum charging voltage of 10.5V, that corresponds to 2.1V for a single capacitor. We have used different working scenarios.
One is that all capacitor begin charging process from the same SOC, and we monitor the individual capacitor evolution. The evolution of voltage starting from the same SOC, in this case zero, is presented in Fig. 10.
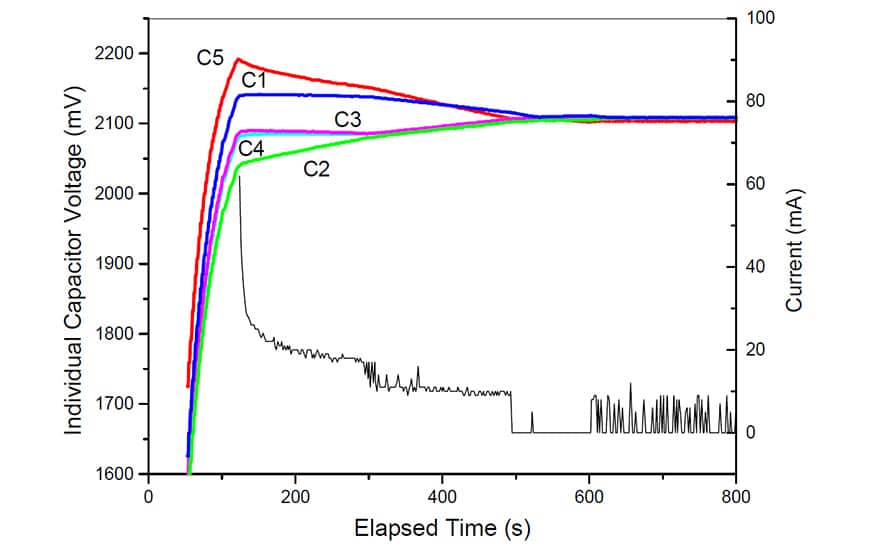
Fig. 10. Voltage evolution for starting with all capacitors (22F) fully discharged
The circuit begins the balancing process just after the charge process is finished, that is the supercapacitor module voltage has reached the programmed value (10.5V) and the flag FC (Full Charge) is set. When the balancing process is started the flag CB is set. During this process a net current is pulsed through the bank, the peak value not exceeding 30mA, as can be seen in Fig. 7. It takes about 600s for a balancing of voltages in the range of ±1mV, which is fairy good. This includes the charging time of the supercapacitors stack.
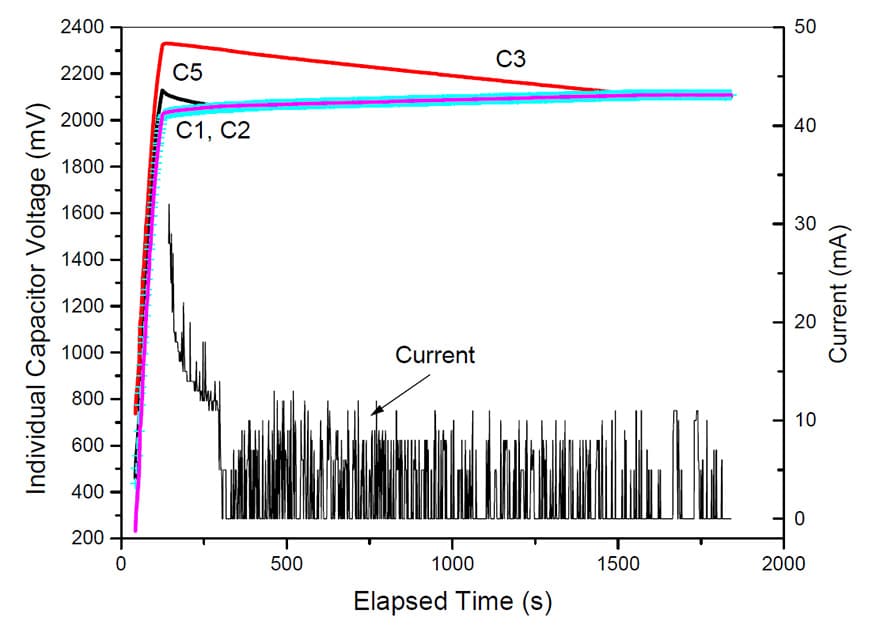
Fig. 11. Voltage evolution for starting with capacitor C3 having 500mV excess voltage
In a different scenario, the supercapacitor C3 (22F) was pre-charged at 700mV, the rest of supercapacitors being set at 200mV, so a difference of 500mV exists, a relatively large imbalance. In this case, the time needed to bring C3 to a voltage of about 2.1V was very long, of about 1600 seconds, as can be seen in Fig. 11.
A different situation, suppose that the charge process starts from voltages of 1.1V except the supercapacitor C2 that was charged at 300mV, so different from previous situation when a capacitor had a larger initial voltage. Now the difference in voltages is 800mV, a very large imbalance, that suggest a possible malfunction of the capacitor. In Fig. 12 are presented the charging curves.
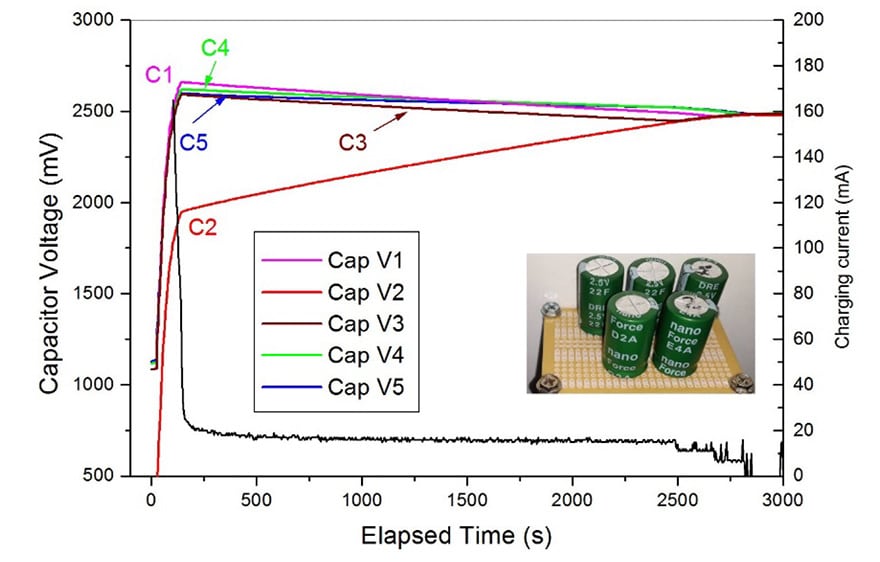
Fig. 12. Voltage and current curves evolution when starting with capacitor C2 having 800mV under voltage
In this case, the time required to balance the voltages of all capacitors is very long, about 2800 seconds. In the case of the 200F supercapacitor module, the balancing was not possible in the limit of ±1mV, but ten times more extensive in the limit of ±10mV, obtainable after more than 1500 seconds starting from the entire charging state. We conclude that the only limit in using higher capacitances is the time needed for charging and balancing.
In Fig. 13 a), the measurement setup shows the PC running the software bqEVSW, connected via USB to the EV2300 SMB module, the evaluation board, and the supercapacitor banks on the left. Fig. 13b) presents a closer view of the bq33100 board.

Fig. 13. a) Measurement setup for evaluating the balancing of supercapacitor modules;
b) evaluation board based on bq33100 circuit
IV. Conclusions
Supercapacitor modules were balanced using the intelligent circuit for monitoring and balancing. The evaluation circuit is performing well, and within 600 seconds, the balancing task for usual unbalancing voltages can appear during operation. In case of more significant differences at the start of the balancing process, more excellent than ±100mV, the process takes more than twice the mentioned time, depending on the initial SOC.
The circuit needs to be modified to balance a supercapacitor module, including 200F capacitors, increasing the charging current and the balancing current, and a higher power capability for the sink load, R27/R28, in Fig. 7.
See also related in-depth technical article on supercapacitor balancing methods and its comparison.
References
[1] http://www.ti.com/lit/ds/symlink/bq33100.pdf, bq33100 datasheet, Texas Instruments, accessed March. 2019.
[2] P. J. Grbovic, Ultra-capacitors in Power Conversion Systems, John Wiley & Sons Ltd, 2014.
[3] C. Ionescu, A. Vasile, R. Negroiu, “Investigations on Balancing Circuits for Supercapacitor Modules”, 39th International Spring Seminar on Electronics Technology (ISSE) Location: Pilsen, Czech Republic,May 18-22, pp 521-526, 2016.
[4] http://www.ti.com/product/BQ33100/toolssoftware, Evaluation Software for bq33100, Texas Instruments, accessed Feb. 2019.
[5] http://www.ti.com/lit/ug/sluu159e/sluu159e.pdf, EV2300 Evaluation Module Interface Board User’s Guide, Texas Instruments, accessed Feb. 2019.
[6] C. Ionescu, A. Drumea, A. Vasile, N. Codreanu, “Investigations on Active Balancing Circuits for Supercapacitor Banks”, 41st International Spring Seminar on Electronics Technology (ISSE), Zlatibor, Serbia, May 16-20, 2018.
- Space-Grade components available for immediate delivery - April 10, 2025
- Exclusive stock on doEEEt: How to access and request - April 10, 2025
- Managing EEE components for LEO and lower cost space missions - December 17, 2024
0 comments on Evaluation of Active Balancing Circuits for Supercapacitors